SELECTED PRINCIPLES: KINETIC THEORY
Diffusion, the movement of particles from a high to low concentration,
and Brownian Motion, the random movement of solid particles suspended
in a liquid or in a gas, are two pieces of evidence which provide the
basis for the kinetic particulate theory of matter - a model which is
used to explain various physical properties of substances.
The main points in the kinetic theory of gases can be summarized as
follows. One, a gas consists of particles in ceaseless random motion.
Two, the volume of the particles themselves is negligible in comparison
with the total volume of the gas. Three, the particles exert neither
attractive nor repulsive forces on one another. Four, the particles
make elastic collisions; i.e., no energy is lost in collisions between
the particles. And five, the average kinetic energy of the particles is
proportional to the absolute temperature of the gas.
Strictly speaking, the kinetic theory refers only to gases. However,
because the difference between the three states of matter is to do with
the amount of energy each state has (i.e., gas > liquid > solid), parts
of the theory are used to provide a model of each of these states; the
Table below summarizes their characteristic properties.
|
SOLIDS |
LIQUIDS |
GASES |
Kinetic energy of particles |
None |
Low |
High |
Motion of particles |
Vibrate about
fixed positions |
Freely around
one another |
Ceaseless
and random |
Rate of diffusion |
Very slow |
Slow |
Fast |
Attractive forces |
Strong |
Fairly weak |
Negligible |
Spacing of particles |
Close contact |
Close contact |
Far apart |
Arrangement of particles |
Regular |
Random |
Random |
Volume |
Fixed |
Fixed |
Variable |
Shape |
Fixed |
Variable |
Variable |
Compressibility |
Virtually
incompressible |
Only slightly
compressible |
Very
compressible |
Density |
High |
High |
Very low |

1. The average kinetic energy, and so the average speed, of molecules
in a gas increases with temperature. Although the derivation of any of
the mathematical equations associated with the kinetic theory of gases
is beyond the scope of this text, advanced studies do show that the
average speed of gas molecules can be calculated using this equation,
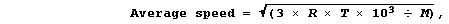
where: R is a constant, with a value of 8.314 J K-¹ mol-¹; T is the
temperature (in K); and, M is the molar mass (in g mol-¹).
Complete this Table, using the equation above to calculate the average
speed of the molecules of these gases at 723 K (450°C).
|
Average speed of molecules / m s-¹ |
Gas |
M / g mol-¹ |
at 298 K |
at 373 K |
at 723 K |
Dihydrogen (H2) |
2 |
1928 |
2157 |
|
Methane (CH4) |
16 |
682 |
763 |
|
Ammonia (NH3) |
17 |
661 |
740 |
|
Carbon monoxide (CO) |
28 |
515 |
576 |
|
Dinitrogen (N2) |
28 |
515 |
576 |
|
Ethene (C2H4) |
28 |
515 |
576 |
|
Ethane (C2H6) |
30 |
498 |
557 |
|
Dioxygen (O2) |
32 |
482 |
539 |
|
Propane (C3H8) |
44 |
411 |
460 |
|
Butane (C4H10) |
58 |
358 |
401 |
|
Sulfur dioxide (SO2) |
64 |
340 |
381 |
|
[7]
2. In everyday-life, water is the substance most commonly observed in
its three physical states (usually known as ice, water, and steam); the
diagram below shows the processes accompanying the physical changes.
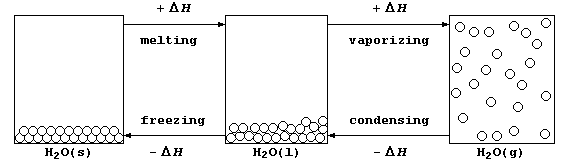
(a) Calculate the heat energy (H) needed to melt one mole of ice at
273 K. [Use the equation H = m × l, where: m is the mass of substance;
and, l is the specific latent heat of fusion of ice, with a value of
0.334 kJ g-¹.] ________________________________________________________
(b) Calculate the heat energy (H) needed to increase the temperature of
one mole of water from 273 to 373 K. [Use the equation H = m × c × DT,
where: m is the mass of substance; c is the specific heat capacity of
water, with a value of 0.00420 kJ g-¹ K-¹; and, DT is the temperature
rise.] ________________________________________________________________
(c) Calcuate the heat energy (H) needed to vaporize one mole of water
at 373 K to steam. [Use the equation H = m × l, where: m is the mass
of substance; and, l is the specific latent heat of vaporization of
water, with a value of 2.26 kJ g-¹.] __________________________________
(d) State the total amount of heat energy released to the surroundings
when one mole of steam at 373 K is converted to ice at 273 K. _________
_______________________________________________________________________
[7]
3. Name the process in which molecules go directly from the solid
into the vapour phase; as is observed, for example, with carbon dioxide
[solid ————® gas]. ___________________________________________________
[1]
Dr. R. Peters Next Contents' List
