AUFBAU1 [EXPERIMENTAL SECTION]
01 Preparation of water-soluble salts using neutralization and metal
displacement reactions
02 The syntheses of compounds structurally related to catalase,
chlorophyll-a, hemoglobin, and vitamin-B12
03 An investigation into the effect of acid concentration on the
speed at which indigestion tablets dissolve in HCl(aq)
04 ... relationship between concentration & conductance of NaCl(aq)
05 ... relationship between the temperature changes of a black-bulb
thermometer as its distance varies from a heat source
06 ... relationship between the heat energy released in displacement
reactions & the potential differences obtained in simple cells
07 ... the dependence of electrical resistance on the diameter and
on the length of nichrome wire
08 ... to determine the relationship between temperature rise & time
when a surface is heated by a radiant heat source
09 ... the effect of temperature on the speed at which a brand of
indigestion tablets dissolves in HCl(aq)
10 ... the specific heat capacities of water-glycerol mixtures
11 ... some variables involved in the inhibition of fungal growth
12 ... relationship between energy released & the concentration of
reactants in a displacement reaction [Al + Cu(II) sulfate(aq)]
13 ... relationship between reaction speed & the concentration of
reactants in a displacement reaction [Mg + HCl(aq)]
14 ... one effect of temperature gradient
15 ... elastic potential energy
16 ... the effect of pH on the germination of seeds
17 ... some variables involved in the heat capacities of solutions
18 ... some variables involved in the cleaning action of detergents
and soap powders
19 ... some variables involved in the decomposition of aqueous
hydrogen peroxide
20 ... some variables involved in the conductivity and electrolysis
of aqueous solutions of metal salts
21 ... some variables involved in the absorption and/or emission of
radiant heat energy
22 ... some variables involved in the germination of seeds
PREPARATION OF WATER-SOLUBLE SALTS USING NEUTRALIZATION AND METAL
DISPLACEMENT REACTIONS
Introduction
Reactions used to prepare salts, which are ionic compounds made up of
ions other than H1+, OH1-, or O2-, include neutralization (i.e., the
reaction between an acid and a base), displacement (i.e., when a more
reactive element displaces a less reactive element from its compound),
and precipitation (i.e., when two soluble ionic compounds react to form
a precipitate). Shown below are equations which summarize exemplars of
these three reaction types; neutralization (1 - 4), displacement (5 and
6), and precipitation (7).
(1) NiO(s) + 2HCl(aq) ——————————————® NiCl2(aq) + H2O(l)
(2) Mg(OH)2(s) + H2SO4(aq) ——————————® MgSO4(aq) + 2H2O(l)
(3) PbCO3(s) + 2HNO3(aq) ————————————® Pb(NO3)2(aq) + H2O(l) + CO2(g)
(4) 2NH3(aq) + H33PO4(aq) ———————————® (NH4)2HPO4(aq)
(5) Zn(s) + H2SO4(aq) ———————————————® ZnSO4(aq) + H2(g)
(6) 2Al(s) + 3Zn(NO3)2(aq) ——————————® 2Al(NO3)3(aq) + 3Zn(s)
(7) 2KOH(aq) + FeSO4(s) —————————————® 2Fe(OH)2(s) + K2SO4(aq)
Whereas a precipitation reaction is commonly used for the preparation
of an insoluble salt, neutralization and metal displacement reactions
are often those of choice for the preparation of water-soluble salts.
[... K > Ca > Na > Mg > Al > Mn > Zn > Fe > Co > Pb > (H) > Cu > Ag ..]
First, using a neutralization reaction, you are required to prepare
crystals of either copper(II) ethanoate or copper(II) chloride, using
appropriate starting materials from: aqueous ethanoic acid; aqueous
sulfuric acid; aqueous hydrochloric acid; copper; copper(II) oxide;
copper(II) carbonate; copper(II) sulfate; and copper(II) nitrate.
And second, using a metal displacement reaction, you are required to
prepare crystals of a second ethanoate or chloride. One starting
material should be some of your freshly prepared copper(II) ethanoate
or copper(II) chloride; and the other should be a suitably correct
choice from: cobalt; cobalt(II) carbonate; manganese; manganese(III)
carbonate; silver; silver(I) carbonate; zinc; and zinc carbonate. |
Before starting your experimental work, be sure to complete this flow
chart - which should summarize your choice of reactants and products.
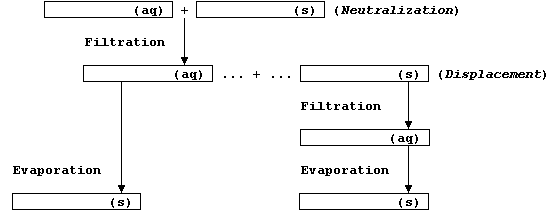
Method (1) - via a Neutralization Reaction
1. Collect the following (for Methods 1 and 2): safety glasses; Bunsen
burner kit; 100 cm³ glass beaker; measuring cylinder (25 cm³); stirring
rod; filter funnel; 2 filter papers; retort stand and clamp; 2 splints;
evaporating dish; 2 petri dishes; pH paper; and starting materials.
2. Set up, ready for use, the Bunsen burner kit and the filtration
apparatus; until required, the evaporation and petri dishes should be
lying face downwards on tissue paper.
3. Using the measuring cylinder, place 25 cm³ of dilute acid into the
beaker equipped with a stirring rod; check the pH of the acid.
4. Warm the acid using a small Bunsen flame (or a boiling water-bath
if a metal is used as one of the starting materials).
5. [Throughout this step, you should be prepared to switch off the
Bunsen if the reaction becomes too vigorous. Furthermore, you should
try and maintain a volume of about 25 cm³ for the reaction mixture, by
adding small volumes of water as and when required.] To the warm acid,
add the solid starting material in small portions until it is in slight
excess; that is, until no more dissolves and the pH paper no longer
turns red.
6. [The reaction mixture contains an excess of insoluble starting
material and the required salt dissolved in water.] Dampen the filter
paper and, using the stirring rod as a guide, filter the warm reaction
mixture into the evaporating dish; it is good technique to wash both
the beaker and filter paper with a little water.
7. [The filtrate (and washings) should contain only the required salt
dissolved in water.] Transfer half the filtrate to a petri dish; cover
this dish with paper, (labeled with name, contents, and date), and
allow the solution to crystallize at room temperature.
8. Using Scotch-tape, attach a small sample of these crystals to this
worksheet; to be safe, you must assume the compound is toxic.
Method (2) - via a Displacement Reaction
1. To the second half of the filtrate (see step 7 above), stir in the
metal powder in small portions until in slight excess; that is, until
there are no more changes to the supernatant.
2. Dampen the filter paper and, using the stirring rod as a guide,
filter this reaction mixture into a second petri dish ....
3. Cover this dish with paper, (labeled with name, contents, and
date), and then allow the solution to crystallize at room temperature.
4. Using Scotch-tape .......... you must assume the compound is toxic.
Notes
Method 1 can be used to prepare most water-soluble salts, providing the
solid starting material, (i.e., metal, oxide, hydroxide, or carbonate),
is insoluble in water. However, a 'titration' method must be used if
the starting material is soluble in water (i.e., all Group 1 compounds,
ammonium compounds, nitrates, and ethanoates).
SYNTHESES OF COMPOUNDS STRUCTURALLY RELATED TO CATALASE, CHLOROPHYLL-a,
HEMOGLOBIN, and VITAMIN-B12
Introduction
In Nature, several dozen compounds contain the porphyrin skeleton, with
varying degrees of unsaturation, bonded to a wide range of functional
groups; examples of these so-called 'porphyrins' include: catalase, an
Fe(II) enzyme which catalyzes the decomposition of cellular hydrogen
peroxide; chlorophyll-a, one of several photosynthetic pigments which
transduce light into chemical energy in plants and other autotrophs;
hemoglobin, the Fe(II) pigment which is responsible for transporting
dioxygen and carbon monoxide in mammals; and vitamin-B12, the Co(III)
cofactor required for the synthesis of mammalian red blood cells.
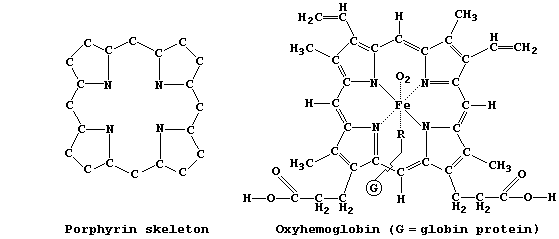
As hinted above, the structures of naturally occurring porphyrins are
very complex. So, in order to study some of their biological, chemical
and physical properties, scientists have synthesized 'simpler' versions
of these molecules; e.g., porphyrins A and B.
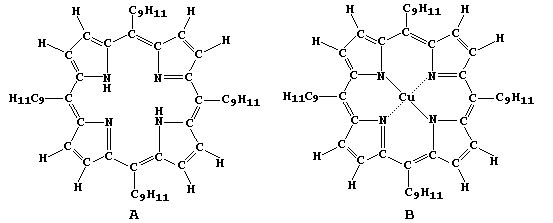
In this four-part series of experiments, you will synthesize copper
ethanoate, free-base porphyrin A, and copper(II) porphyrin B - from
porphyrin A and copper ethanoate - as well as examine porphyrins A
and B using chromatography. |
Method (Part 1) - Synthesis of Hydrated Copper(II) Ethanoate
1. Using a measuring cylinder, place 25 cm³ of dilute ethanoic acid
(1 mol dm-³) into a small beaker equipped with a stirring rod.
2. Warm the acid using a small Bunsen flame.
3. To the warm acid, add copper(II) carbonate in small portions until
in excess; i.e., until no more carbonate dissolves, there is no further
evolution of gas, and universal indicator paper no longer turns red.
4. Using a filter paper, filter the warm mixture; be sure to wash the
beaker and paper with a little distilled water.
5. Using a boiling water-bath, concentrate the copper(II) ethanoate
solution to about half its original volume.
6. Transfer the concentrated solution to a petri dish; then allow the
hydrated copper(II) ethanoate to crystallize at room temperature.
Method (Part 2) - Synthesis of Porphyrin A
1. Using a measuring cylinder, place 40 cm³ of propanoic acid into a
100 cm³ Pyrex beaker.
2. Using a hot plate contained in a fume-cupboard, carefully heat the
propanoic acid until it just starts to boil.
3. Using separate graduated (or automatic) pipets, simultaneously
add pyrrole (1.0 cm³) and 4-isopropylbenzenecarbaldehyde (2.0 cm³).
4. Continue gently boiling this reaction mixture for 7 minutes; then
allow it to cool overnight.
5. Using a sintered-glass crucible, filter the mixture; then wash the
beaker and crystals with ethanoic acid (3 pasteur pipet measures),
followed by methanol (4 p.p.m.).
6. Dry free-base porphyrin A before placing it in a sample tube.
Method (Part 3) - Synthesis of Copper(II) Porphyrin B
1. Weigh about 0.10 g of porphyrin A into a small beaker; then add
trichloroethane (15 cm³).
2. Weigh about 0.10 g of hydrated copper(II) ethanoate into another
small beaker; then add methanol (15 cm³).
3. Using a hot plate (or a water-bath), separately heat both of the
above solutions until each is gently boiling.
4. Add the hot methanol solution to the trichloroethane solution; then
continue boiling for about 3 minutes.
5. Using a sintered-glass crucible, filter the mixture; then wash the
beaker and precipitate with warm methanol (3 p.p.m.), followed by warm
distilled water (4 p.p.m.).
6. Dry copper(II) porphyrin B before placing it in a sample tube.
Method (Part 4) - Chromatography of Porphyrins A and B
1. Using trichloroethane, freshly prepare separate solutions of both
porphyrins (A and B).
2. Develop the chromatograms of both porphyrins, using the same piece
of chromatography paper, in methanol:trichloroethane (5:1 ?).
Notes, Results (and Extension Work)
1. Copper(II) ethanoate crystallizes from an aqueous solution as the
mono-hydrate, Cu(CH3COO)2.H2O; i.e., copper(II) ethanoate-water(1/1).
2. Attach a sample of each compound and the best resolved chromatogram
to this worksheet, using Scotch-tape. Then, using a microscope, examine
the shapes and the colors (!) of your crystals.
3. Examine the catalytic behavior, if any, of each compound; e.g.,
the decomposition of aqueous sodium chlorate(I), the decomposition of
aqueous hydrogen peroxide, the reaction of zinc with dilute sulfuric
acid, ... {Each porphyrin can be 'bulked-up' as follows: dissolve a
measured quantity of porphyrin in trichloroethane; stir in a measured
quantity of an 'inert' carrier [e.g., aluminum oxide, carbon-graphite,
or silicon(IV) oxide]; and then allow to evaporate to dryness.}
AN INVESTIGATION INTO THE EFFECT OF ACID CONCENTRATION ON THE SPEED AT
WHICH INDIGESTION TABLETS DISSOLVE IN HYDROCHLORIC ACID
Introduction
Digestion is the name given to the series of physical and chemical
processes by which complex insoluble foods are hydrolyzed to simple
soluble substances that can be absorbed into the bloodstream. Dilute
hydrochloric acid provides the acidic conditions necessary for stomach
enzymes to continue the digestive process that starts in the mouth;
however, an excess of stomach acid results in 'indigestion'. Tablets
containing a base - such as aluminum hydroxide, calcium carbonate,
magnesium hydroxide, or sodium hydrogencarbonate - are available which
relieve indigestion by partially neutralizing the excess acid; e.g.,
2HCl(aq) + CaCO3(s) ——————————® CaCl2(aq) + H2O(l) + CO2(g)
In this investigation, you are required to examine two related
hypotheses.
Hypothesis 1: The time (T) taken for __________ indigestion tablets
to dissolve in aqueous hydrochloric acid is in linear proportion to
the concentration (C) of the acid; i.e., T = k × C + c.
Hypothesis 2: The speed (S) of dissolving of __________ indigestion
tablets in aqueous hydrochloric acid is in linear proportion to the
concentration (C) of the acid; i.e., S = k × C + c. |
Method
1. Using a reference thermometer, measure room temperature.
2. Using a measuring cylinder, place 25 cm³ of aqueous hydrochloric
acid (2.00 mol dm-³) into a scrupulously clean beaker.
3. Simultaneously, add one tablet to the acid and start the clock.
4. Stop the clock when the tablet has completely dissolved.
5. Repeat steps 2 to 4, but each time use a different concentration of
acid; the water should be at the same temperature as the stock solution
of acid, and the volume of water should be measured using a separate
measuring cylinder.
6. Repeat steps 2 to 5 for appropriate duplicate experiments.
7. Using the reference thermometer, re-measure room temperature.
Table of Results and Calculations
Constants: room temperature (_____); initial concentration of acid
(2.00 mol dm-³); volume of solution (25 cm³); brand of indigestion
tablets (__________); surface area of each tablet (_____); mass of
each tablet (_____); absence of catalysts. |
Volume of
HCl(aq)
/ cm³ |
Volume of
H2O
/ cm³ |
Final Conc. of
HCl(aq) (C)
/ mol dm-³ |
Time for tablet
to dissolve (T)
/ s |
Speed of tablet
dissolving (S)
/ ms-¹ |
25 |
0 |
2.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
20 |
0.40 |
|
|
|
|
|
|
|
[Speed (S), the inverse of time (i.e., T-¹), is calculated using
either of these equally correct equations: speed (in s-¹) = 1 ÷ time
(in s) or speed (in ms-¹) = 1000 ÷ time (in s).] |
Graphs
1. Plot all data points of a first graph, with the dependent variable
of time (T) on the vertical axis. Draw a best line through as many
points as is sensible; here, you should obtain a curve.
2. The tabulated data and this first graph should provide the evidence
for this conclusion: "In the absence of catalysts, the time (T) taken
for one whole __________ tablet to dissolve at room temperature (_____)
decreased as the concentration (C) of aqueous hydrochloric acid
increased (within the range ____________ mol dm-³). The curve indicates
that these two variables are not in linear proportion to each other;
i.e., T ‡ k × C + c."
3. Plot all data points of a second graph, with the dependent variable
of speed (S) on the vertical axis. As here you should obtain a straight
line, determine its gradient (units are ms-¹ mol-¹ dm³); this value,
'k', is the proportionality constant in the linearly proportional
relationship S = k × C + c.
Sources of Error and Calculation
Broadly speaking, experimental work can be considered to include three
types of error: systematic (e.g., those arising from inaccuracies in
each instrument used); random or observational (e.g., those arising
from inaccuracies in reading each instrument); and design (i.e., those
introduced by assumptions inherent in the experimental method).
1. Name the instruments which introduce systematic errors into these
experiments. __________________________________________________________
2. Estimate reasonable values for the probable errors in your reading
of each of these instruments. _________________________________________
3. Suggest one or more possible errors inherent in the experimental
method. _______________________________________________________________
_______________________________________________________________________
4. Use the second graph to form a second, precisely worded conclusion
from your investigation. ______________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
Notes
1. To gain an outline of the range of results, it is often useful to
to measure first the dependent variable for the largest and smallest
values of the independent variable; in this investigation, for example,
these are C = 2.00 mol dm-³ and 0.40 mol dm-³, respectively.
2. To be able to determine confidently a relationship between two
variables, it is necessary to measure the dependent variable for at
least five values of the independent variable; in this investigation,
for example, a reasonable choice would be C = 2.00, 1.60, 1.20, 0.80,
and 0.40 mol dm-³. [For absolute rigor, a control experiment could be
be executed; that is, C = 0.00 mol dm-³.]
3. To minimize experimental errors, as well as to gain some idea of
the reproducibility of both method and technique, it is necessary to
execute duplicate (or confirmatory) experiments. There are two methods
of choosing 'duplicates': either arbitrarily selecting the middle value
of the independent variable (in this investigation, for example, this
would be C = 1.20 mol dm-³); or, with scientific rigor, examining the
raw data for a value of the dependent variable which does not follow
the general pattern (the detection of this value, known as an anomalous
result, occasionally requires drawing a sketch graph).
AN INVESTIGATION INTO THE RELATIONSHIP BETWEEN THE CONCENTRATION AND
THE CONDUCTANCE OF AQUEOUS SODIUM CHLORIDE
Introduction
Studies have shown that, in order to conduct electricity, a substance
must contain either free-moving electrons or free-moving ions; an ion
is either a charged atom or a charged group of atoms (e.g., ammonium
and hydrogencarbonate). In the solid state, an ionic compound consists
of a lattice of oppositely charged ions which are not free to move
because they are held together by strong electrostatic attractions.
However, when an ionic compound is either melted or dissolved in water,
these ions are free to move, and so the electrolyte formed does conduct
an electric current.
Directly or indirectly, conductance is important in a variety of
scientific contexts; e.g., nerve impulses, electroplating, electrical
cells, and the extraction of metals by electrolytic reduction.
Quite reasonably, one might expect the conductance of an aqueous ionic
compound to be dependent on several independent variables, including
the concentration of dissolved compound ...
In this investigation, you are required to examine this hypothesis:
As the concentration (M) of sodium chloride increases, within the
range 0.00 - 1.00 mol dm-³, the conductances (C) of the aqueous
solutions increase in direct proportion; i.e., C = k × M. |
Method
1. Using a measuring cylinder, measure out 100 cm³ of aqueous sodium
chloride (1.00 mol dm-³) into a clean beaker.
2. Construct the circuit shown below, as follows: connect the series
part first, ensuring that the positive output (+) of the d.c. source is
connected to the positive input (+) of the ammeter ('red' to 'red');
then connect the voltmeter in parallel.
3. Set the d.c. output source to a constant value (about 6 V ?).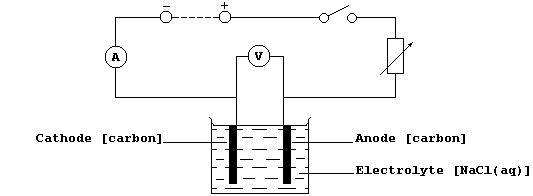
4. Close the switch, and immediately record the readings of both the
ammeter and the voltmeter; if a meter reads below zero, then the
polarities are reversed.
5. Open the switch, and record the following values: temperature of
the solution; depth of the immersed electrodes; and distance between
the anode and cathode. These values should remain constant throughout
the following step.
6. Ensuring that you clean and dry the electrodes between each set of
readings, separately measure the current and voltage for the other
available concentrations and for appropriate duplicates.
Table of Results and Calculations
Constants: _________________________________________________________
____________________________________________________________________
____________________________________________________________________ |
Concentration (M)
/ mol dm-³ |
Current (I)
/ A |
Voltage (V)
/ V |
Conductance (C)
/ W-¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Conductance (C) = Current (I) ÷ Voltage (V)] |
Graphs
1. Plot all the points of a well-labeled graph; i.e., complete with
units and with a precisely worded title. Draw a best line through as
points as is sensible; and then determine whether, broadly speaking,
the graph is a straight line (go to 2), or a straight line and a curve
(go to 3), or a curve (go to 4).
2. If the graph is a straight line, determine its gradient 'k' (which
has the units ohm-¹ mol-¹ dm³). If this straight line passes through
the origin, then 'k' is the proportionality constant in the directly
proportional relationship C = k × M (valid for the concentration range
0.00 - 1.00 mol dm-³).
3. If the graph is a straight line and a curve, determine the gradient
of the straight line portion; this value, 'k', is the proportionality
constant in the linearly proportional relationship C = k × M + c (valid
for the concentration range __________ mol dm-³).
4. If the graph is a curve, then these two variables are not in simple
proportion to each other; i.e., C ‡ k × M + c (over the concentration
range __________ mol dm-³).
Notes (and Extension Work)
1. The SI unit for conductance is the siemen (S), but the equivalent
unit of W-¹ is more commonly used (perhaps because it emphasizes
that conductance is the inverse of resistance).
2. A graph shows direct proportionality between two variables, X and
Y, if it is a straight line that passes through the origin (i.e., X =
0.0 and Y = 0.0); mathematically, this direct relationship is expressed
as Y = k × X, where 'k' is the proportionality constant.
3. A graph shows linear proportionality between two variables, X and
Y, if it is a straight line that does not pass through the origin; this
linear relationship is expressed as Y = k × X + c, where 'k' is the
proportionality constant, and 'c' is the intercept on the Y-axis.
4. A graph shows no simple proportionality between two variables, X
and Y, if it is a curve; this absence of simple proportionality is
expressed either as Y ‡ k × X, or, more generally, as Y ‡ k × X + c.
5. Complete this investigation, as follows. First, after considering
the various sources of error, write a critical evaluation. Second,
construct one or more precisely worded conclusions. And third, suggest
a reasonable interpretation of the results.
6. Many substances are classified either as 'ohmic' conductors or, if
their resistances change with voltage, as 'non-ohmic' conductors.
Consider planning (and executing) an investigation which examines, over
the voltage range 5 - 12 V, the ohmic characteristics of aqueous sodium
chloride (1.00 mol dm-³).
AN INVESTIGATION INTO THE RELATIONSHIP BETWEEN THE TEMPERATURE CHANGES
OF A BLACK-BULB THERMOMETER AS ITS DISTANCE VARIES FROM A HEAT SOURCE
Introduction
Radiant heat energy, in the form of electromagnetic waves, is emitted
from hot bodies (e.g., the Sun, light bulbs, and living organisms). A
detailed knowledge of the variables which affect the absorption of this
energy is necessary to understand a variety of phenomena, including
'the use of (renewable) solar energy to heat buildings', 'homeostasis
in ectotherms', 'photochemical reactions', and 'the detection of prey
by certain predators (e.g., snakes)'.
The amount of radiant energy absorbed by a surface is well known to be
affected by a number of independent variables; these include the total
and type of energy emitted from the heat source, the distance of the
surface from the source, the color of the surface, and its luster
(i.e., whether the surface is shiny or dull). However, to investigate
quantitatively the effect of any one of these independent variables,
all of the others must be both measured and held constant.
Consider, as a specific example, the following qualitative hypothesis:
As the distance of a thermometer decreases from a heat source, so does
its temperature rise. A quantitative investigation of this hypothesis
requires that only the independent variable of interest is changed
(i.e., distance): all other independent variables must be both measured
and held constant (i.e., room temperature, heat source, time, and type
of thermometer).
Using a 0-50°C black-bulb thermometer heated by a 100 W light bulb
for 180 s, you are required to investigate two related hypotheses.
Hypothesis 1: As the distance (D) increases, within the range 0.060-
0.140 m, the temperature rise (DT) decreases in linear proportion;
i.e., DT = k × D + c.
Hypothesis 2: As the inverse-square of the distance (D-²) increases,
within a distance range of 0.060-0.140 m, the temperature rise (DT)
increases in linear proportion; i.e., DT = k × D-² + c. |
Method
1. Using a reference thermometer, measure room temperature.
2. Carefully clamp a 0-50°C black-bulb thermometer at a measured
height from the bench.
3. Place a 100 W light bulb, fitted in a holder, 0.060 m from this
thermometer; this distance (D) is measured, using a pair of dividers,
from the light bulb side-surface to the bulb of the thermometer.
4. Measure the starting temperature of the black-bulb thermometer to
the nearest 0.1°C.
5. Simultaneously, switch on the light bulb and start the clock.
6. After exactly 180 seconds, measure the final temperature (again to
the nearest 0.1°C); you will need to keep one eye on the thermometer
and one eye on the clock.
7. Repeat steps 2 to 6 for the other distances suggested in the Table,
using the same starting temperature; thus, cool the thermometer to
below this value, clamp it in position, and then allow it to reach the
required starting temperature.
8. Repeat steps 2 to 6 twice more for the distance D = 0.100 m, again
using the same starting temperature.
9. Finally, to determine whether the temperature gradient has changed,
use the reference temperature to re-measure room temperature.
Table of Results and Calculations
Constants: __________________________________________________________
_____________________________________________________________________
_____________________________________________________________________ |
Distance
(D) / m |
Distance-²
(D-²) / m-² |
Starting Temp.
/ °C |
Final Temp.
/ °C |
Temp. rise
DT / °C |
0.060 |
|
|
|
|
0.080 |
|
|
|
|
0.100 |
|
|
|
|
0.100 |
|
|
|
|
0.100 |
|
|
|
|
0.120 |
|
|
|
|
0.140 |
|
|
|
|
Graphs
1. Plot all seven points of a first graph, with the dependent variable
(DT) on the vertical axis. Draw a best line through as many points as
is sensible; here, you should obtain a smooth curve.
2. The tabulated data and this first graph should provide the evidence
for this conclusion: "At room temperature (_____), the temperature rise
(DT) of a dull-black bulb thermometer, heated for ______ by a ______
light bulb, decreased as the distance (D) increased (within the range
of _________). The curve indicates that these two variables are not in
in linear proportion to each other; i.e., DT ‡ k × D + c."
3. A curve is, however, less mathematically convenient than a straight
line; to generate the latter, it is often necessary to consider other
forms of an independent variable x: for example, x², x³, x-¹, x-², ...
4. Calculate the data for a different form of the independent variable
(D-²), and then use these values to plot a second graph; draw a best
line through as many points as is sensible. As here you should obtain
a straight line, determine its gradient (units are °C m²); this value,
'k', is the proportionality constant in the inverse-square relationship
DT = k × D-² + c.
Sources of Error and Calculations
Broadly speaking, experimental work can be considered to include three
types of error: systematic (e.g., those arising from inaccuracies in
each instrument used); random or observational (e.g., those arising
from inaccuracies in reading each instrument); and design (i.e., those
introduced by assumptions inherent in the experimental method).
1. The clock, ruler, and thermometer are all sources of systematic
error. Estimate reasonable values for the probable errors in your
reading of each of these instruments. _________________________________
2. Remembering that the thermometer is read twice in obtaining DT,
calculate and then compare the percentage errors for the measurement of
time, D, and DT when D = 0.140 m. _____________________________________
_______________________________________________________________________
_______________________________________________________________________
3. Suggest one or more possible errors inherent in the experimental
method. _______________________________________________________________
_______________________________________________________________________
4. Use both the Table and the second graph to form a precisely worded
conclusion in respect of Hypothesis 2. ________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
AN INVESTIGATION INTO THE RELATIONSHIP BETWEEN THE HEAT ENERGY RELEASED
IN METAL DISPLACEMENT REACTIONS AND THE POTENTIAL DIFFERENCES OBTAINED
IN SIMPLE ELECTRICAL CELLS
Introduction
Chemically, a metallic element (M) is characterized by its tendency to
lose one or more electrons and form a positive ion; i.e., it is readily
oxidized (Olé!): M ———————————® Mn+ + ne-
Quite reasonably, one might hypothesize that 'different metals will have
different tendencies to lose electrons and form stable positive ions'.
Indeed, measured heat energy changes in displacement reactions and
potential differences in simple electrical cells, amongst a wide variety
of data, have provided convincing evidence to support this hypothesis.
All chemical and biochemical reactions involve an energy change; e.g.,
chemical energy may be transduced to electrical, kinetic, light, sound,
or (most often) to heat energy. Chemical to heat energy changes occur,
for example, in displacement reactions such as:
M(s) + Cu2+(aq) ————————————® Mn+(aq) + Cu(s) (if M › Cu)
In such redox reactions, electrons are transferred from metal atoms to
copper(II) ions because the metal is more reactive than copper (i.e.,
the metal is more easily oxidized); the redox half equations are:
M(s) ———————————® Mn+(aq) + ne- (oxidation)
Cu2+(aq) + 2e- ———————————® Cu(s) (reduction)
Chemical to electrical energy changes occur, for example, in simple
electrical cells; thus, using the apparatus shown below, a potential
difference (V) is observed if the metal (M) is more or less reactive
than copper.
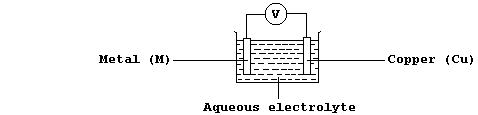
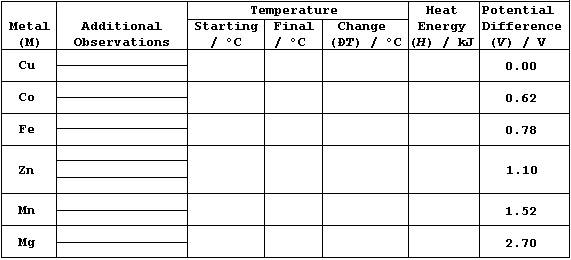
[.. Ca > Mg > Al > Mn > Zn > Fe > Co > Ni > Sn > (H) > Cu > Ag > Pd ..]
In this investigation, you are required to examine two relationships.
First, that between the metal reactivity series & the heat energy (H)
released in metal displacement reactions involving aqueous copper(II)
sulfate. And second, that between the heat energy (H) released & the
potential differences (V) observed in simple electrical cells of the
type metal/copper (M/Cu); in particular, whether H = k × V. |
Method
1. Using a reference thermometer, measure room temperature.
2. Using a bulb-pipet equipped with a safety-filler, or a buret,
or a measuring cylinder, place 25.0 cm³ of aqueous copper(II) sulfate
(0.200 mol dm-³) into an insulated plastic cup; then measure the
starting temperature of the solution to at least the nearest 0.2°C.
3. Add a slight excess of zinc powder to the cup; boldly, but gently,
stir the mixture; and then measure the highest temperature reached.
4. Record any changes in the reaction mixture; e.g., the color of the
solution and of the (precipitated) solid.
5. Ensuring that the cup is clean, and that both the insulation and
the cup are dry, repeat steps 2 to 4 for the duplicates of zinc, then
the control (copper), and finally the other metals listed in the Table.
6. Using the reference thermometer, re-measure room temperature.
Results and Calculations
Constants: ____________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
1. Potential difference data (V), for M/Cu, have been edited from
values compiled by A. J. Bard et al. (Standard Potentials in Aqueous
Solutions, Marcel Dekker, New York, 1985).
2. The heat energy released from a chemical reaction can be determined
by first measuring its temperature change, and then using the equation
H = m × c × DT, where: H is the heat energy released; m is the mass of
substance; c is its specific heat capacity; and DT is the temperature
change.
3. If the mass of 25.0 cm³ of aqueous copper(II) sulfate is assumed
to be 0.025 kg, and if its specific heat capacity is assumed to be the
same as that of pure water (i.e., 4.2 kJ kg-¹ °C-¹), then the above
equation simplifies to: H = 0.025 × 4.2 × DT.
Graphs
1. Plot well-labeled bar graphs of these data: one dependent variable
(H) should be a linear scale on the left vertical axis, the other
dependent variable (V) should be a linear scale on the right vertical
axis, and the independent variable should be on the horizontal axis
(with each metal as a separate block); use one block for zinc, with its
average value for H obtained either from all three results, if they are
acceptably close together, or from the two closest results.
2. Plot all eight points of a well-labeled line graph of these data;
consider the dependent variable to be heat energy released (H) and the
independent variable to be potential difference (V). Draw a best
straight line through the origin and as many points as is sensible, and
then determine its gradient; this value, 'k', is the proportionality
constant in the directly proportional relationship H = k × V.
Sources of Error and Conclusions
Complete this investigation, as follows. First, after considering the
various sources of error (i.e., systematic, random, and design), write
a critical evaluation (and, perhaps, include one or more suggestions as
to how the errors could be minimized). Second, after considering the
errors, the two bar graphs, and the line graph, construct one or more
precisely worded conclusions. And third, predict how much heat energy
(H) would be released (if any) for the reactions of calcium, nickel,
and palladium with aqueous copper(II) sulfate - using, in part, these
data: Ca/Cu = 3.20 V; Ni/Cu = 0.58 V; and Pd/Cu = -0.65 V.
AN INVESTIGATION INTO THE DEPENDENCE OF ELECTRICAL RESISTANCE ON THE
DIAMETER AND ON THE LENGTH OF NICHROME WIRE
Introduction
The resistance of a conductor is well known to be dependent upon the
material it is made from, its length, diameter, and temperature: but,
quantitative relationships between the variables need to be determined
by controlled experiments ...
In this investigation, using the so-called voltmeter-ammeter method,
you are required to examine the dependence of resistance (R) on the
diameter (D) and on the length (L) of Nichrome wire - in particular,
to determine the validity of the following relationships:
R = k × D + c; R = k × D-¹ + c; R = k × L + c; R = k × L-¹ + c. |
Method
1. Construct the circuit shown below, with the d.c. output set to a
constant value (about 4.5 V ?).
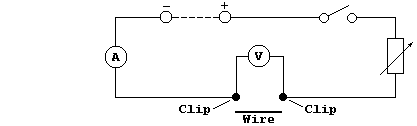
2. Measure 0.270 m of Ni-Cr resistance wire of one chosen diameter; if
this value is not known, the wire should be measured with a micrometer.
Place the inside of each crocodile clip 0.010 m away from each end of
the wire, so that the effective length of wire is 0.250 m.
3. Close the switch and immediately record the readings of both the
ammeter and the voltmeter; then open the switch.
4. Using an effective length of 0.250 m, repeat steps 2 and 3 for each
diameter wire (within the range 0.28 - 0.56 mm) and, after examining
the raw data, for appropriate duplicates.
5. Finally, for wire of one chosen diameter, modify steps 2 to 4 so as
to obtain similar data for differing lengths of wire (within the range
of 0.100 - 0.400 m).
Tables of Results and Calculations
Constants (for independent variables D and D-¹): ___________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________ |
Diameter
(D) / mm |
Diameter-¹
(D-¹) / mm-¹ |
Voltage
(V) / V |
Current
(I) / A |
Resistance
(R) / W |
Power
(P) / W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Resistance = Voltage ÷ Current Power = Voltage × Current]
Constants (for independent variables L and L-¹): ___________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________ |
Length
(L) / m |
Length-¹
(L-¹) / m-¹ |
Voltage
(V) / V |
Current
(I) / A |
Resistance
(R) / W |
Power
(P) / W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Notes (and Extension Work)
1. Complete this investigation, as follows. First, construct a graph
for each independent variable; you will need to truncate both axes for
each graph. Second, write a critical evaluation. Third, construct a
precisely worded conclusion for each of the investigated relationships.
And fourth, suggest one or more interpretations of the results.
2. The wires used in the National Grid system carry very high voltages
and fairly high currents over long distances, so they must be thick in
order to minimize losses of 'low-grade' heat energy; therefore, cheap,
low-density aluminum is used rather than expensive, high-density
copper (although this metal has a lower resistance, and so lower losses
in conducting electrical energy). Consider investigating some aspects
of 'resistance heating', by examining the dependence of power (P) on
various independent variables (... using a graph/statistics program?).
AN INVESTIGATION TO DETERMINE THE RELATIONSHIP BETWEEN TEMPERATURE RISE
AND TIME WHEN A SURFACE IS HEATED BY A RADIANT HEAT SOURCE
Introduction
Extensive studies have shown that the amount of radiant energy absorbed
by a surface is affected by a number of independent variables; these
include the total and type of energy given out from the heat source,
the distance of the surface from the source, the color of the surface,
and its luster (i.e., whether the surface is shiny or dull).
Preliminary studies have shown that the temperature rise (DT) of a
dark-colored surface, over a period of 300 seconds, is related to time
(t) by the following linear relationship:

where 'k' is a proportionality constant, 'n' is an index, and 'c' is a
constant. However, the 'best' value for 'n' remains to be established;
in principle, a combination of experimental and graphical methods can
be used to obtain this value ...
Using raw data collected by the experimental method described, the
focus of your investigation is determine whether there is evidence
to support one of the following hypotheses.
Hypoth. 1: The temperature rise of a surface is in linear proportion
to the time exposed to radiant heat energy; i.e.,  Hypoth. 2: The temperature rise of a surface is in linear proportion
to the square root of the time exposed to radiant heat energy; i.e.,  Hypoth. 3: The temperature rise of a surface is in linear proportion
to the cube root of the time exposed to radiant heat energy; i.e.,  Hypoth. 4: The temperature rise of a surface is in linear proportion
to the fourth root of the time exposed to radiant heat energy; i.e.,  |
Method
1. Using a reference thermometer, measure room temperature.
2. Carefully clamp a 0-50°C black-bulb thermometer at a measured
height from the bench.
3. Place a 100 W light bulb 0.060 m away from this thermometer; this
distance is measured, using a pair of dividers, from the light bulb
side-surface to the bulb of the thermometer.
4. Measure the starting temperature of the black-bulb thermometer to
the nearest 0.1°C.
5. Switch on the 100 W light bulb, and record the temperature every
60 seconds for 300 seconds.
6. Repeat step 5 twice more, using the same starting temperature;
thus, cool the thermometer to below this value, clamp it in position,
and then allow it to reach the required starting temperature.
7. Finally, to determine whether the temperature gradient has changed,
use the reference thermometer to re-measure room temperature.
Table of Results and Calculations
Constants:_____________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________

[The average value for DT is obtained either from all three results, if
they are acceptably close together, or from the two closest results.]
Notes
Complete this investigation, as follows. First, construct a graph for
each form of the independent variable (with a gradient if appropriate);
you will need to truncate the horizontal axis when the variable is the
square-root, cube-root, or fourth-root of time (t). Second, write a
critical evaluation. And third, construct a precisely worded conclusion
for each form of the independent variable.
AN INVESTIGATION INTO THE EFFECT OF TEMPERATURE ON THE SPEED AT WHICH
INDIGESTION TABLETS DISSOLVES IN AQUEOUS HYDROCHLORIC ACID
Introduction
Digestion is the name given to the series of physical and chemical
processes by which complex insoluble foods are hydrolyzed to simple
soluble substances that can be absorbed into the bloodstream. Dilute
hydrochloric acid provides the acidic conditions necessary for stomach
enzymes to continue the digestive process that starts in the mouth;
however, an excess of stomach acid results in 'indigestion'. Tablets
containing a base - such as aluminum hydroxide, calcium carbonate,
magnesium hydroxide, or sodium hydrogencarbonate - are available which
relieve indigestion by partially neutralizing the excess acid; e.g.,
2HCl(aq) + CaCO3(s) ——————————® CaCl2(aq) + H2O(l) + CO2(g)
The homeostatic temperature of the stomach is roughly 37°C. However,
significant variations from this temperature will inevitably result
from ingesting liquids and foods, and such variations might reasonably
be expected to affect the physical and chemical processes of digestion.
In this investigation, you are required to examine the hypothesis
that: Within the range ________°C, the speed (S) of dissolving of
brand ____________ indigestion tablets in aqueous hydrochloric acid
(2.00 mol dm-³) is in linear proportion to the temperature (T) of
the acid; i.e., S = k × T + c'. |
Method
1. Collect a _____°C thermometer, and measure room temperature; then
compare this value with that obtained using an accurate reference
thermometer.
2. Using the available insulating material, make a jacket that will
fit a small glass beaker.
3. Using a measuring cylinder, or a bulb-pipet equipped with a
safety-filler, or a buret, place 25.0 cm³ of dilute hydrochloric acid
(2.00 mol dm-³) into a scrupulously clean beaker.
4. Place the beaker into the 'home-made' insulating jacket.
5. Measure the temperature of the acid; then, simultaneously, add one
tablet to the acid and start the clock.
6. Stop the clock when the tablet has completely dissolved; and then
immediately record the temperature again.
7. Repeat steps 3 to 6, but each time change the temperature of the
acid (within the range _____°C), using either an ice-bath or a heat
source.
8. Finally, after carefully examining your raw data for any anomalous
results, carry out appropriate duplicate experiments.
Notes
1. Both the insulating jacket and the outside of the beaker must be
absolutely dry for each experiment.
2. For the present investigation, you will need to use this equation:
speed (in ms-¹) = 1000 ÷ time (in s).
3. Your write-up should include, in addition to a complete summary of
your results and conclusions presented in the most suitable form, a
critical evaluation of your investigation.
4. The rates of chemical reactions are affected by several independent
variables, including both the concentration and surface area of the
reactants. So, show on the graph paper, using appropriately labeled
sketch lines, how you would expect the speed of reaction to change by:
(a) using more dilute hydrochloric acid; and (b) crushing the tablets.
AN INVESTIGATION INTO THE SPECIFIC HEAT CAPACITIES OF WATER-GLYCEROL
MIXTURES
Introduction
The physical and chemical properties of water differ from those of most
other liquids, but make it uniquely effective in supporting living
activities; e.g., water has the highest heat capacity of any liquid,
which means that it can absorb a lot of heat without the temperature
rising to levels which would denature cellular proteins.
However, water does have two properties which are certainly not optimal
for organisms living in certain environments. First, it freezes at 0°C:
so various animals which live in very cold habitats need some sort of
'anti-freeze', because the rate of diffusion is exceptionally slow in
frozen cells. And second, it has the highest water potential: so plants
which live in very salty habitats need a substance which will counter-
balance the low water potential of the external environment, otherwise
their cells would lose water by exo-osmosis. For some organisms (e.g.,
the algae Dunaliella), the biochemical solution to these differing
'problems' of water is to incorporate glycerol into their cytoplasm.
In this investigation, you are required to examine this hypothesis:
As the concentration (C) of glycerol increases, the specific heat
capacities (c) of the aqueous solutions decrease in direct
proportion; i.e., c = k × C. |
Method
1. Measure the mass of an insulated plastic cup; add about 150 cm³ of
water; measure the mass of the cup and water; and, finally, subtract
these two masses to determine the mass of water (in kg).
2. Place a 12 V a.c. heater at a measured depth in the liquid, wait a
few minutes, and then record the starting temperature (in K).
3. The circuit for these experiments will already be constructed, so
close the switch and record the amount of energy (in kJ) required to
raise the temperature of the gently stirred liquid by 12 K; be careful
not to touch the heater with the thermometer.
4. Repeat steps 1 to 3 for each concentration of glycerol; i.e., 20%,
40%, 60%, and 80% (... and appropriate duplicates ...).
Notes
1. Shown below are the structural formulae of water, ethanol, ethane-
1,2-diol, and propane-1,2,3-triol (glycerol). These three alcohols are
miscible with water; their solubility is partially attributable to
'hydrogen bonding' [i.e., the weak electrostatic attraction between the
nucleus of a bonded hydrogen atom and a 'lone-pair' of electrons of a
bonded non-hydrogen atom (typically, nitrogen or oxygen)].

2. You will need to use this equation c = H ÷ (m × DT), where: c is
the specific heat capacity; H is the heat energy supplied; m is the
mass of substance; and DT is the temperature rise.
3. Your write-up should include, in addition to a complete summary of
results and calculations, a critical evaluation, a precisely worded
conclusion, and a suggested interpretation of the results.
AN INVESTIGATION INTO SOME OF THE VARIABLES INVOLVED IN THE INHIBITION
OF FUNGAL GROWTH
Introduction
Kingdom Fungi contains all the multi-cellular absorptive heterotrophs;
i.e., those living organisms which obtain their nutrients by the extra-
cellular, enzymic digestion of organisms and the subsequent absorption
of soluble ions and molecules by diffusion.
The importance of fungi in recycling essential nutrient ions for the
autotrophs is well-established; and, furthermore, may be of increasing
importance because the precipitation of 'acid rain' has resulted in
acidic environments and the release of soluble (metal) ions. Moreover,
as this Table shows, fungi are significant organisms in everyday-life.
Fungus or Fungi |
Notes |
Saccharomyces |
Yeasts used in the baking, brewing, and
fuel industries; uni-cellular ! |
Rhizopus stolonifer |
Usually known as 'black bread mold'. |
Puccinia |
Cause 'rust' diseases on crops. |
Fusarium |
Used in the manufacture of SCP; nutrient
source is paper or cereal plant waste. |
Plasmopara viticola |
Causes 'downy mildew' on grapes; aqueous
copper(II) sulfate will act as a fungicide. |
Aspergillus |
Cause athlete's foot and ringworm. |
Mucor mieleli |
Biosynthesizes enzyme chymosin (rennin)
which is suitable for the manufacture of
vegetarian cheeses. |
Penicillium roqueforti |
Used to 'ripen' blue-veined cheeses. |
Penicillium notatum |
Biosynthesizes the antibiotic penicillin. |
The 'anti-social behavior' of Rhizopus stolonifer fungus hints at one
important aspect of fungal growth: namely, food preservation. Because
fungi are typical living organisms with cellular metabolism controlled
by enzymes, most methods of preserving food have focused on directly or
indirectly inhibiting the activities of these enzymes.
Methods of direct inhibition include refrigeration and 'pickling' in an
acidic medium. Thus, low temperatures result in substrate and enzyme
particles having less kinetic energy, and so fewer have the required
activation energy for successful collisions: whereas, aqueous hydrogen
ions [i.e., H1+(aq)], which diffuse into cells across semi-permeable
membranes, denature a variety of enzymes.
Methods of indirect inhibition, which focus on the removal of the water
required for diffusion of substances in to and out of cells, include
immersion in a preservative with a low water potential (e.g., brine or
sugar syrup); here, water is removed from fungal cells by exo-osmosis
across semi-permeable membranes.
However, as perhaps also hinted at previously, a broader knowledge of
the variables involved in the growth and inhibition of fungi is clearly
of wider importance ...
In this investigation, using bread as a substrate and (sealed) petri
dishes as safe containers, you are required to examine at least three
variables involved in the inhibition of fungal growth; at least two
of these must be quantitative, and at least one must be qualitative. |
Notes
1. A qualitative variable is one that is non-numerical (or purely
descriptive); e.g.,
(dependent), the color of the mycelium of hyphae [... black, brown,
gray, red, white],
(independent), the type of potential inhibitor [... absent ('control'),
copper(II) sulfate, ethanoic acid, phenol, sodium chloride].
2. A quantitative discontinuous variable is one where the data are
obtained by counting, and so are whole numbers; e.g.,
(dependent), the number of spore cases present after 168 hours [... 96,
85, 74, 47, 40],
(independent), the number of drops of pond water added to the substrate
[... 4, 3, 2, 1, 0].
3. A quantitative continuous variable is one where the data are
obtained by measuring, and so can take any value within a continuous
range; e.g.,
(dependent), the area of fungal growth after 168 hours [... 2.07, 1.59,
1.43, 1.42, 1.35 cm²],
(independent), the concentration of aqueous copper(II) sulfate added
to the substrate [... 1.00, 0.75, 0.50, 0.25, 0.00 mol dm-³ or ...
1.000, 0.100, 0.010, 0.001, 0.000 mol dm-³].
4. For each hypothesis, in order 'to isolate the (chosen) independent
variable', it is essential that the values of all the other independent
variables are measured and kept constant.
5. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias and data bases on CD-ROM; it is good
practice to include a bibliography in your write-up.
6. You are provided with bread substrates, stock solutions of a wide
variety of substances, distilled water, petri dishes, and Scotch-tape.
In addition, you will need to use - within reason - other apparatus you
consider to be necessary.
7. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
8. Apart from the standard use of safety glasses, and possibly gloves,
two safety precautions are vitally important: first, the fully labeled
petri dishes, once sealed, must not be opened during the investigation;
and second, these dishes must be disposed of by incineration at the end
of the investigation.
AN INVESTIGATION INTO THE RELATIONSHIP BETWEEN THE ENERGY RELEASED AND
THE CONCENTRATION OF REACTANTS IN A DISPLACEMENT REACTION
Introduction
A displacement reaction is the chemical change which occurs when a more
reactive element displaces a less reactive element from its compound;
e.g., 2Al(s) + 3CuSO4(aq) ——————————® Al2(SO4)3(aq) + 3Cu(s)
In this redox reaction, electrons are transferred from aluminum atoms
to copper(II) ions because aluminum is a better reducing agent (i.e.,
it is more easily oxidized); the redox half equations are:
2Al(s) ———————————® 2Al3+(aq) + 6e-
3Cu2+(aq) + 6e- ———————————® 3Cu(s)
The aqueous sulfate ions are spectators, so the net ionic equation is:
2Al(s) + 3Cu2+(aq) ———————————® 2Al3+(aq) + 3Cu(s)
[.. K > Ca > Na > Mg > Al > Zn > Fe > Sn > Pb > (H) > Cu > Hg > Ag ..]
For the reaction of aluminum with aqueous copper(II) sulfate, in the
presence of sodium chloride, you are required to investigate whether
there is a direct relationship between the heat energy released and
the concentration of aqueous copper(II) sulfate; i.e., H = k × C ? |
Notes
1. Aqueous chloride ions facilitate the removal of the very thin oxide
layer which invariably covers aluminum: however, they do not catalyze
the reaction between (pure) aluminum and aqueous copper(II) sulfate.
2. The heat energy released from a chemical reaction can be determined
by first measuring its temperature change, and then using the equation
H = m × c × DT, where: H is the heat energy released; m is the mass of
substance; c is its specific heat capacity; and DT is the temperature
change. [Assume that 1.00 cm³ of aqueous copper(II) sulfate has a mass
of 0.001 kg, and that its specific heat capacity is 4200 J kg-¹ K-¹.]
3. You are provided with aluminum powder, aqueous copper(II) sulfate
(with an initial concentration of 0.300 mol dm-³), distilled water, and
sodium chloride. In addition, you will need to use - within reason -
suitable apparatus.
4. The proposed plan of your investigation should be presented in
detail; this plan may be modified as the investigation proceeds.
AN INVESTIGATION INTO THE RELATIONSHIP BETWEEN REACTION SPEED AND THE
CONCENTRATION OF REACTANTS IN A DISPLACEMENT REACTION
Introduction
A displacement reaction is the chemical change which occurs when a more
reactive element displaces a less reactive element from its compound;
e.g., Mg(s) + 2HCl(aq) ——————————® MgCl2(aq) + H2(g)
In this redox reaction, electrons are transferred from magnesium atoms
to copper(II) ions because magnesium is a better reducing agent (i.e.,
it is more easily oxidized); the redox half equations are:
2Mg(s) ———————————® Mg2+(aq) + 2e-
2H1+(aq) + 2e- ———————————® H2(g)
The aqueous chloride ions are spectators, so the net ionic equation is:
Mg(s) + 2H1+(aq) ———————————® Mg2+(aq) + H2(g)
Independent variables known to change the speeds of chemical reactions
include concentration, temperature, surface area, and the presence of
catalysts. However, the determination of quantitative relationships
between such variables requires careful experimentation ...
[.. K > Ca > Na > Mg > Al > Zn > Fe > Sn > Pb > (H) > Cu > Hg > Ag ..]
For the displacement reaction of magnesium with aqueous hydrochloric
acid, you are required to investigate three hypotheses.
Hypothesis 1: The reaction time (T) is in direct proportion to the
acid concentration (C); i.e., T = k × C.
Hypothesis 2: The reaction speed (S) is in direct proportion to the
acid concentration (C); i.e., S = k × C.
Hypothesis 3: The reaction speed (S) is in direct proportion to the
acid concentration squared (C²); i.e., S = k × C². |
Notes
1. The speed of a reaction can be investigated by measuring the time
taken for a fixed amount of either one of the reactants to disappear or
one of the products to appear; speed = 1 ÷ time or, more conveniently,
speed (in ms-¹) = 1000 ÷ time (in s).
2. You are provided with magnesium ribbon, aqueous hydrochloric acid
(with an initial concentration of 1.00 mol dm-³), and distilled water.
In addition, you will need to use - within reason - suitable apparatus.
3. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
AN INVESTIGATION INTO ONE EFFECT OF TEMPERATURE GRADIENT
Introduction
The Principle of the Conservation of Energy states that "energy is
neither created nor destroyed, but can be transduced from one form to
another". All energy transductions release heat energy; and when this
is transferred to the surroundings, it is described as 'low-grade' and
is usually considered to be 'lost'.
Not surprisingly, both the loss of heat energy and its control is of
practical importance in industry, machines, laboratory experiments,
homes, and in living organisms. Accordingly, a detailed knowledge of
the effects of the independent variables involved in the rate of heat
energy transfer is of similar importance.
Quite reasonably, one might expect these variables to include the
method of energy transfer (e.g., conduction, convection, or radiation),
the substances involved (and their surface areas), and the temperature
gradient between the system and its surroundings ...
In this investigation, within a temperature gradient range of 5-48°C,
you are required to examine the effect of temperature gradient on the
rate of energy transfer. |
Notes
1. You will need to use the equations H = m × c × DT and P = H ÷ t,
where: H is the heat energy transferred; m is the mass of substance; c
is its specific heat capacity; DT is the temperature change; P, power,
is the rate of heat energy transfer; and t is the time.
2. You are provided with sources of hot and cold water, crushed ice,
measuring cylinders, a 100 cm³ glass beaker, a 250 cm³ plastic beaker,
a 0-50°C thermometer, and a clock. In addition, you may need to use -
within reason - other suitable apparatus.
3. The proposed plan of your investigation should be presented in
detail; this plan may be modified as the investigation proceeds.
AN INVESTIGATION INTO ELASTIC POTENTIAL ENERGY
Introduction
Strictly speaking, there are only two forms of energy: namely, kinetic
and potential. However, both forms can be conveniently divided into
various types; e.g., chemical, elastic, gravitational, and nuclear are
all types of potential energy.
Elastic potential energy is stored in a number of substances (e.g., in
compressed springs, stretched rubber, and compressed gases), and then
transduced into kinetic energy (e.g., in clockwork toys, trampolines,
and combustion engines); as with all energy transductions, there is
also a transfer of 'low-grade' heat energy to the surroundings.
Despite the availability of well-established equations to measure
energy (e.g., elastic potential energy = 0.5 × force × extension), it
is often necessary to determine new relationships by experiment ...
Using a combination of experimental and graphical methods, you are
required to investigate the relationship between the extension (E) of
a rubber band and the distance (D) moved by a missile; in particular,
to determine which of the following relationships is most valid:
D = k × E; D = k × E-1; D = k × E0.5; D = k × E2 |
Notes and Extension Work
1. You are provided with a block of wood, callipers, thumbtacks,
graph paper, 'missiles', newtonmeter, rubber bands, and rulers. In
addition, you may use - within reason - other suitable apparatus.
2. The proposed plan of your investigation should be presented in
detail; this plan will almost certainly need to be modified as the
investigation proceeds, because initial attempts to obtain reproducible
results are usually unsuccessful (... 'patience is a virtue' ...).
3. [Extension: To determine the most valid relationship will involve
keeping all but one of the independent variables constant. Investigate
the effect of another independent variable on the value of 'k'.]
AN INVESTIGATION INTO THE EFFECT OF pH ON THE GERMINATION OF SEEDS
Introduction
The development, dispersal, and germination of seeds represents part of
the complex structures and mechanisms by which flowering plants ensure
successful reproduction; this is important, because the only purpose of
these living organisms is to ensure that some or all of their genes are
passed onto future generations. Furthermore, as producers, flowering
plants provide - via photosynthesis - the chemical energy required by
consumers and decomposers:
Light / Chlorophylls / Enzymes
6CO2(g) + 6H2O(l) ———————————————————————® C6H12O6(aq) + 6O2(g) +DE
Seeds vary enormously in size and internal structure. Nevertheless, the
structure of a typical seed is as follows: an embryo, consisting of a
young shoot (the plumule), a young root (the radicle), and one or more
seed leaves (the cotyledons), surrounded by a seed coat (the testa).
Careful experiments have established that, for successful germination,
seeds have three requirements: water (to allow diffusion); dioxygen (to
ensure that enough energy, in the form of ATP, is released via aerobic
respiration); and a suitable temperature (to promote enzyme activity).
Enzymes
C6H12O6(aq) + 6O2(g) —————————————————————® 6CO2(g) + 6H2O(l) -DE
Less well established, however, are the effects of other independent
variables; in view of the increasing levels of acidic pollution, pH
might reasonably be considered one of these.
In this investigation, you are required to examine the effect of pH
on the success and/or rate of seed germination. |
Notes
1. Germination is considered to be complete when the seedling has
formed its first green leaves; these allow it, via the process of
photosynthesis, to synthesize its own chemical energy by transducing
light energy.

3. Depending on the weather conditions and location, 'acid rain' can
have a pH of between 2.2 and 5.5: whereas unpolluted rainwater, which
is effectively a dilute solution of carbonic acid, has a pH of 5.6.
4. You are provided with solutions of varying pH, a variety of seeds,
and growth substrates (including tissue and compost). In addition, you
will need to use - within reason - other suitable apparatus.
5. The proposed plan of your investigation should be presented in
detail; this plan may be modified as the investigation proceeds.
AN INVESTIGATION INTO SOME OF THE VARIABLES INVOLVED IN THE THERMAL
CAPACITIES OF AQUEOUS SOLUTIONS
Introduction
Pure water is a covalently bonded compound with some unusual physical
properties; these include a high boiling point, a high surface tension,
a maximum density as a liquid, a high latent heat of vaporization, and
the highest thermal capacity of any liquid.
However, pure water is rarely encountered in Nature because it is such
an excellent solvent in which many solutes dissolve to varying degrees.
Furthermore, the resulting aqueous solutions might quite reasonably be
expected to have different properties; e.g., thermal capacities.
A detailed knowledge of variables involved in the thermal capacities of
aqueous solutions should be important in order to understand a variety
phenomena, such as 'homeostatic control of temperature within cells',
or 'the effect of global warming on aquatic organisms living in saline
environments', or 'the use of sea water as an external coolant', or ...
In this investigation, you are required to examine at least three
variables involved in the thermal capacities of aqueous solutions;
at least one of these must be quantitative, and at least one must
be qualitative. |
Notes
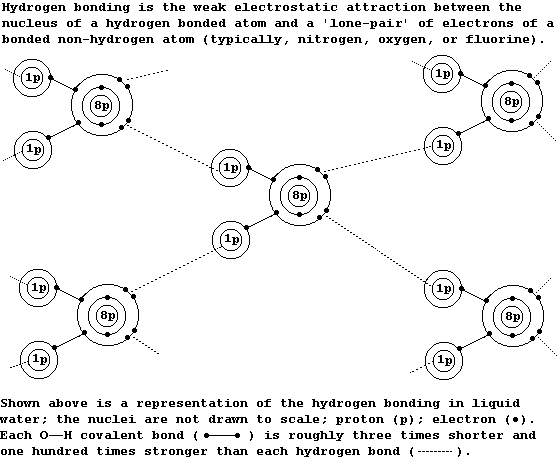
1. All of these properties of water are partially attributable to its
extended structure, which involves 'hydrogen bonding'; although many
molecules show hydrogen bonding, (including ammonia, DNA, ethanol,
propane-1,2,3-triol, and most enzymes), each water molecule is unique
in its ability to hydrogen bond with four other water molecules.
2. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias in libraries, on CD-ROMs, and on the
Web; it is good practice to include a bibliography in your write-up.
3. You are provided with a variety of compounds, distilled water, a
joulemeter, and a direct current supply. In addition, you will need to
use - within reason - other suitable apparatus.
4. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
AN INVESTIGATION INTO SOME VARIABLES INVOLVED IN THE CLEANING ACTION
OF COMMERCIALLY AVAILABLE SOAP POWDERS AND DETERGENTS
Introduction
Washing products were introduced to simplify the chore of washing
clothes. Since their introduction, manufacturers have continuously
attempted to persuade the general public that their particular product
is, in some way or another, «best». However, «best» may refer to:
value for money; and/or
washes clothes the cleanest; and/or
colorr fastness; and/or
the inclusion of a free measuring cup or a plastic toy; and/or
biological action (i.e., the product contains enzymes which speed up
the washing process at low temperatures); and/or
environmental friendliness (i.e., the product is biodegradable); and
...........................?
Surprisingly, perhaps, manufacturers do apply the scientific method to
support their claims - even if their choice of variables is, on
occasions, a shade selective ...
In this investigation, you are required to examine at least three
variables involved in the cleaning action of one or more washing
products; two of these must be independent variables. |
Notes
1. Apart from your notes and standard textbooks, useful sources of
information might include the labels on washing products and fabrics;
it is good practice to include a bibliography in your write-up.
2. You are provided with a variety of washing products, fabrics, and
stains. In addition, you will need to use - within reason - suitable
apparatus.
3. The proposed plans of your investigation should be presented in
detail; these plans may be modified as a result of trial or complete
sets of experiments.
AN INVESTIGATION OF SOME OF THE VARIABLES INVOLVED IN THE DECOMPOSITION
OF AQUEOUS HYDROGEN PEROXIDE
Introduction
Hydrogen peroxide is a toxic excretion product from certain metabolic
reactions in living cells; accordingly, its removal is essential to
ensure survival of a living cell or an organism.
Aqueous hydrogen peroxide decomposes slowly at ambient temperatures,
but published studies have shown that its decomposition is speeded up
by the enzyme catalase and by various inorganic catalysts [such as
manganese(IV) oxide]: Catalase or MnO2
2H2O2(aq) ————————————————® 2H2O(l) + O2(g)
In this investigation, you are required to examine at least three
variables involved in the decomposition of aqueous hydrogen peroxide;
at least two of these must be quantitative. |
Notes
1. Each enzyme is assigned a numerical classification (as approved by
the international scientific organizations); catalase, for example, is
E.C. (Enzyme Commission) 1.11.1.6.
2. Despite differences in size and complexity, all living organisms
show remarkable similarity in biochemical reactions; and so, as might
be expected, catalase is present in most of these organisms. However,
extraction of the pure enzyme is tedious - so most investigations use
convenient sources (e.g., liver, potato, or yeast).
3. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias in libraries, on CD-ROMs, and on the
Web; it is good practice to include a bibliography in your write-up.
4. You are provided with 30% aqueous hydrogen peroxide, sources of the
enzyme catalase (e.g., potato), a variety of inorganic substances, and
distilled water. In addition, you will need to use - within reason -
suitable apparatus.
5. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
AN INVESTIGATION INTO SOME VARIABLES INVOLVED IN THE CONDUCTIVITY AND
THE ELECTROLYSIS OF AQUEOUS SOLUTIONS OF METAL SALTS
Introduction
Studies have shown that, in order to conduct electricity, a substance
must contain either free-moving electrons or free-moving ions; an ion
is either a charged atom or a charged group of atoms (e.g., ammonium
and hydrogencarbonate). In the solid state, an ionic compound consists
of a lattice of oppositely charged ions which are not free to move
because they are held together by strong electrostatic attractions.
However, when an ionic compound is either melted or dissolved in water,
these ions are free to move, and so the electrolyte formed does conduct
an electric current.
Directly or indirectly, conductivity is important in a wide variety of
scientific contexts; e.g., nerve impulses, electroplating, electrical
cells, and the extraction of metals by electrolytic reduction.
Sea water is an important natural resource because it is rich in water-
soluble metal salts (e.g., LiI, NaCl, and MgBr2). The extraction of
pure substances from sea water involves a series of physical processes
(e.g., evaporation and fractional crystallization), as well as chemical
processes (in particular, electrolysis; i.e., the decomposition of an
electrolyte by an electric current, as a result of redox reactions
which occur at electrodes). So, quite reasonably, a knowledge of the
effects of the variables involved in the electrolysis of metal salts is
important (not least because the process uses vast amounts of expensive
electrical energy).
A few semi-quantitative relationships between some variables have been
determined (see the three examples summarized in Note 1). Nevertheless,
purely quantitative relationships for a wide range of variables are not
readily available ...
In this investigation, you are required to examine at least four
variables involved in the conductivity and/or electrolysis of aqueous
solutions of metal salts; at least two of these variables must be
quantitative, and at least one must be qualitative. |
Notes
1. The three examples are as follows. One, at room temperature (23°C),
using carbon-graphite electrodes at a depth of 46 mm and a distance of
7 mm, the conductance (C) of 100 cm³ of NaCl(aq), when a small voltage
is applied (~6.0 V), is in inverse proportion to concentration (M;
within the range 0.20 - 0.80 mol dm-³); i.e., C = k × M-¹ + c.
Two, the resistance (R) of 0.45 mm diameter nichrome wire, when a small
voltage is applied (~5.0 V), is in linear proportion to length (L;
within the range 0.15 - 0.40 m); i.e., R = k × L + c.
And three, the rate of energy transfer (P) in 0.20 m of nichrome wire,
when a small voltage is applied (~5.0 V), is in inverse proportion to
diameter (D; within the range 0.35 - 0.55 mm); i.e., P = k × D-¹ + c.
2. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias in libraries, on CD-ROMs, and on the
Web; it is good practice to include a bibliography in your write-up.
3. You are provided with different types of electrodes (e.g., carbon-
graphite, copper, and iron), various aqueous solutions of metal salts
and acids (each with an initial concentration of 1.00 mol dm-³), a low-
voltage d.c. supply, and a range of electrical components. In addition,
you will need to use - within reason - other suitable apparatus.
4. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
AN INVESTIGATION INTO SOME OF THE VARIABLES INVOLVED IN THE ABSORPTION
AND/OR EMISSION OF RADIANT HEAT ENERGY
Introduction
Radiant heat energy, in the form of electromagnetic waves, is emitted
from hot bodies (e.g., the Sun, light bulbs, and living organisms). A
detailed knowledge of the variables which affect the absorption and the
emission of this energy is necessary to understand various phenomena,
including 'homeostasis in ectotherms', 'photochemical reactions', and
'the detection of prey by certain predators (e.g., snakes)'.
The amount of radiant energy absorbed by a surface is well known to be
affected by a number of independent variables; these include the total
and type of energy emitted from the heat source, the distance of the
surface from the source, the color of the surface, and its luster
(i.e., whether the surface is shiny or dull). However, there appears
to be relatively few details concerning the quantitative relationships
between possible variables - though four are summarized in Note 1.
In this investigation, you are required to examine at least four
variables involved in the absorption and/or emission of radiant heat
energy; at least three of the variables must be quantitative, and at
least one must be qualitative. |
Notes
1. Four relationships involving either the absorption or emission of
radiant heat energy are as follows.
First, Stefan-Boltzman's Law: the energy radiated from a black body
is proportional to the fourth power of the body's absolute temperature
(T); i.e.,

Second, Wien's Law: the wavelength carrying the maximum energy is
inversely proportional to the body's absolute temperature (T); i.e.,

Third: the temperature rise of a black-bulb thermometer, heated by a
standard 100 W light bulb for 180 s, is proportional to the inverse-
square of the distance (D; within the range of 0.06 - 0.14 m); i.e.,

And fourth: the temperature rise of a yellow-, green-, or purple-bulb
thermometer, heated at a distance of 0.060 m by a standard 100 W
light bulb, is roughly proportional to the fourth root of time (t;
within the range 0 - 240 s); i.e.,

2. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias in libraries, on CD-ROMs, and on the
Web; it is good practice to include a bibliography in your write-up.
3. You are provided with clear-film, LDRs, light bulbs, paints, metals,
mirrors, photo-paper, thermometers, and thermistors; in addition, you
will need to use - within reason - other suitable apparatus.
4. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
AN INVESTIGATION INTO SOME OF THE VARIABLES INVOLVED IN THE GERMINATION
OF SEEDS
Introduction
The development, dispersal, and germination of seeds represents part of
the complex structures and mechanisms by which flowering plants ensure
successful reproduction; this is important, because the only purpose of
these living organisms is to ensure that some or all of their genes are
passed onto future generations. Furthermore, as producers, flowering
plants provide - via photosynthesis - the chemical energy required by
consumers and decomposers:
Light / Chlorophylls / Enzymes
6CO2(g) + 6H2O(l) ———————————————————————® C6H12O6(aq) + 6O2(g) +DE
Seeds vary enormously in size and internal structure. Nevertheless, the
structure of a typical seed is as follows: an embryo, consisting of a
young shoot (the plumule), a young root (the radicle), and one or more
seed leaves (the cotyledons), surrounded by a seed coat (the testa).
Careful experiments have established that, for successful germination,
seeds have three requirements: water (to allow diffusion); dioxygen (to
ensure that enough energy, in the form of ATP, is released via aerobic
respiration); and a suitable temperature (to promote enzyme activity).
Enzymes
C6H12O6(aq) + 6O2(g) —————————————————————® 6CO2(g) + 6H2O(l) -DE
However, the effects of other independent variables on either the rate
or success of seed germination remain to be established; a detailed
knowledge of these variables is necessary in view of increasing levels
of pollution.
In this investigation, you are required to examine at least four
variables involved in the germination of seeds; at least two of these
must be quantitative, and at least one must be qualitative. |
Notes
1. Apart from your notes and standard textbooks, sources of scientific
knowledge include encyclopedias in libraries, on CD-ROMs, and on the
Web; it is good practice to include a bibliography in your write-up.
2. You are provided with several varieties of seeds [including cabbage
(Brassica oleracea), cress (Lepidum spp.), lettuce (Latuca spp.), mung
beans (Phaseolus aureus), mustard (Brassica nigra), rape (Brassica
rapa), pea (Pisum savitum), and sunflower (Helianthus annus)], plant
growth regulators, enzymes, aqueous solutions of salts and acids (each
with an initial concentration of 0.20 mol dm-³), growth substrates, and
light sources. In addition, you will need to use - within reason -
suitable apparatus.
3. The proposed plans of your investigation should be presented in
detail; these plans may be modified as the investigation proceeds.
_______________________________________________________________________
_______________________________________________________________________
Comedy-Dramas for Year 10-12 Students in American Orthography :
[No. 1] [No. 2] [No. 3] [No. 4] [No. 5] [No. 6] [No. 7] [No. 8] [No. 9]
[Dr. Roger Peters : rpeters@wissensdrang.com ; Aufbau1 ; Home Page]










